Ratios and fractions are very similar things, since they are both arise from comparing the relative sizes of quantities. Let’s quickly review what exactly a fraction is. If you think of a “whole” as made up of some number of equal parts (e.g. a group of people, a sliced cake, a regularly marked length of wood), a fraction tells you how many of those parts you need to consider. It is written as a pair of numbers ![]() , and the number above the line, called the numerator, tells you how many parts, while the number below the line, called the denominator, tells you how many parts in the whole. So, for example,
, and the number above the line, called the numerator, tells you how many parts, while the number below the line, called the denominator, tells you how many parts in the whole. So, for example, ![]() means 1 of 3 equal parts.
means 1 of 3 equal parts.
Ratios are a more flexible representation of relative quantities because they quote a direct comparison. You do not need equal parts, or integer values, or even only two values. In the case of ![]() there is 1 part taken, and 2 parts left over, so as a direct comparison of quantities we see this value is equivalent to the ratio 1:2 — say “1 to 2″. This is well illustrated using the circle below. The fraction shaded green is one third, and the ratio of green to yellow is 1:2. The fraction tells us one part of the three is green, while the ratio tells us that there is twice as much yellow as there is green — two ways of saying exactly the same thing.
there is 1 part taken, and 2 parts left over, so as a direct comparison of quantities we see this value is equivalent to the ratio 1:2 — say “1 to 2″. This is well illustrated using the circle below. The fraction shaded green is one third, and the ratio of green to yellow is 1:2. The fraction tells us one part of the three is green, while the ratio tells us that there is twice as much yellow as there is green — two ways of saying exactly the same thing.
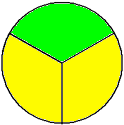
To convert from the ratio 1:2 back to a fraction, we need to think about how much we have (1 part) out of the total (1 part + 2 parts = 3 parts), to get
![]()
Unlike fractions, ratios are often used to compare non-integer values — 0.2:0.5 and ![]() are both perfectly valid ratios. In addition, ratios are can be used to compare more than 2 values, for example the ratio 5:12:13 might be used to describe the relative lengths of the sides of a triangle. You could use this ratio to draw up a triangle with sides 5cm, 12cm and 13cm, or alternatively one with sides of 10cm, 24cm and 26cm, or any other multiple of those original three numbers. And, as I discuss in the section on scaling below, every one of those triangles would have exactly the same shape. (Another thing about those particular triangles is they would all be right angled. Do you know why?)
are both perfectly valid ratios. In addition, ratios are can be used to compare more than 2 values, for example the ratio 5:12:13 might be used to describe the relative lengths of the sides of a triangle. You could use this ratio to draw up a triangle with sides 5cm, 12cm and 13cm, or alternatively one with sides of 10cm, 24cm and 26cm, or any other multiple of those original three numbers. And, as I discuss in the section on scaling below, every one of those triangles would have exactly the same shape. (Another thing about those particular triangles is they would all be right angled. Do you know why?)
When quoting a ratio, the order of the numbers is important. The ratios 1:9 and 9:1 are very different. Imagine that you are mixing flour and water in each ratio. In the first case there would be much more water than flour, 9 times as much — that’s what the ratio means, and you’d have a very runny mixture. In the second case there’d be 9 times more flour than water, and the mixture would be essentially powder.
It is also very important to be completely clear on what is being compared. A ratio of flour to water of 1:9 says that in every 10 parts of mixture, 1 part is flour, and 9 parts are water. It is also possible to consider the ratio of flour to total quantity, which would be is 1 part flour to 10 parts mixture, or 1:10. In the special case of a ratio of part to whole, and only in this special case, the connection between ratios and fractions is very clear, and the ratio 1:10 is equivalent to the fraction ![]() .
.
Ratios and the Birth of Mathematics
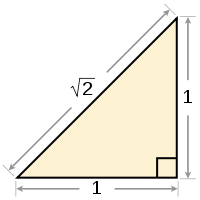
In Ancient Greece in the 6th century BC, amongst the Pythagoreans, the concept of ratio played a fundamental role in the development of pure mathematics. Numbers, in their conception, were restricted to just the counting numbers, 1, 2, 3 etc. Everything else arose from measurement, i.e. comparing directly to a standard unit, and were thus ratios. It was around these concepts that mathematics developed. The Pythagoreans were particularly perturbed to discover that the ratio of the length of the diagonal to the length of a side of a unit square (i.e. a square with side length 1 unit) could not be “measured”. The actual value is ![]() , and in modern parlance we say it is irrational — it cannot be written as a fraction, or an integer ratio. Legend has it that the poor fellow who told the world of this dark and shameful secret was drowned for his crime.
, and in modern parlance we say it is irrational — it cannot be written as a fraction, or an integer ratio. Legend has it that the poor fellow who told the world of this dark and shameful secret was drowned for his crime.
Ratio was also central to the Pythagorean’s understanding of harmony. They discovered that two strings with lengths in the ratio 2:1 are the same note, separated by an octave. Similarly, a length ratio of 4:3 generates a perfect fourth, and 3:2 a perfect fifth.
Equivalent Ratios
Just like
![]()
are all equivalent fractions, multiplying each term in a ratio by the same number produces an equivalent ratio
![]()
The relative sizes stay the same, or, as we say in everyday language, “in the same ratio”. The second number is exactly twice the first in every case. As long as you multiply all numbers in a ratio by the same value, the ratio is unchanged. The numbers remain in the same proportion.
You can practice converting ratios to their simplest equivalent at The Mathenæum.
Ratios and Scaling
Maintaining proportion in this way is the essence of scaling. Think about images — as long as every length in a picture is multiplied by the same factor, the objects in the picture look the same. Circles stay round, the aspect ratio of rectangles is unaltered. If instead we scaled horizontally by twice as much as we scaled vertically (think about resizing an image on a computer) everything would get stretched in the left and right directions, and the picture would look very different!
We can see this happen with the following simple picture.  Scaling down to half size makes a smaller copy, but everything in the picture has exactly the same shape, and the ratio of any length in our new picture to the corresponding length in the original picture is 1:2 — that is the original lengths are all twice the new lengths.
Scaling down to half size makes a smaller copy, but everything in the picture has exactly the same shape, and the ratio of any length in our new picture to the corresponding length in the original picture is 1:2 — that is the original lengths are all twice the new lengths.  If instead we scaled down by a factor of two in the vertical direction, but up by a factor of two in the horizontal direction, things appear very different. Our horizontal lengths are now all twice as long as their originals, i.e. the ratio of new to original is 2:1, whereas the vertical lengths are only half as long, i.e. the ratio of new to original is 1:2, and the internal shapes have all changed.
If instead we scaled down by a factor of two in the vertical direction, but up by a factor of two in the horizontal direction, things appear very different. Our horizontal lengths are now all twice as long as their originals, i.e. the ratio of new to original is 2:1, whereas the vertical lengths are only half as long, i.e. the ratio of new to original is 1:2, and the internal shapes have all changed. 
A Ratio Puzzle
A famous puzzle states:
An old man decides to divide his camels between his three children in the ratio
, and
. Given that the man owns 11 camels (and he does not intend to slice any of them up!) how many must he give to each son?
See if you can find the solution.
Click to show/hide the "trick" answer
The trick answer to the puzzle is that the man borrows 1 camel from his neighbour to get 12 camels in all. The first son gets half of the 12, which is 6 camels. The second son gets one quarter of the 12, i.e. 3 camels, and the third son gets one sixth, or 2 camels. 11 camels have thus been distributed, and the one camel left over is simply returned to the neighbour.
The puzzle relies on the easy confusion between ratio and fraction. The old man is not giving the first son half of his camels — that would be 5½ camels and is clearly unsatisfactory. It is the relative sizes that we need to consider. So what the three fractions are really telling us is that the first son gets twice what the second son gets because ![]() is twice
is twice ![]() . Remember — ratios are direct comparisons. Similarly, the first son’s share is three times the third son’s share, because
. Remember — ratios are direct comparisons. Similarly, the first son’s share is three times the third son’s share, because ![]() .
.
The easiest way to work it out is to simplify the ratio — get rid of the fractions. We can do that by finding the Least Common Multiple (LCM) of the denominators, and multiplying all three terms.
Let’s do the calculation now. The first few multiples of 2 are 2, 4, 6, 8, 10, 12…, the first few multiples of 4 are 4, 8, 12, 16…, and the first few multiples of 6 are 6, 12, 18…. So, the LCM is 12, and multiplying all terms by 12 will give us an equivalent ratio that does not include any fractions.
![Rendered by QuickLaTeX.com \[\begin{array}{ccccc} \frac{1}{2} & : & \frac{1}{4} & : & \frac{1}{6} \\ \color{red}{\scriptstyle \times 12} & & \color{red}{\scriptstyle \times 12} & & \color{red}{\scriptstyle \times 12} \\ 6 & : & 3 & : & 2 \end{array}\]](../../../../wp-content/ql-cache/quicklatex.com-4f0b29d1abc8223436d2bef83530dc15_l3.png)
That is, the ratios ![]() :
: ![]() :
: ![]() and
and ![]() are equivalent. Since there are 11 camels, and
are equivalent. Since there are 11 camels, and ![]() , the distribution is straightforward.
, the distribution is straightforward.
Why the old man didn’t just use this form of the ratio directly remains a mystery…
Bamboozler: Dehydrating Potatoes — where did all that weight go?
Now we can finish with a nice, ratio-based bamboozling that is known as the Potato Paradox.

You have 100kg of Martian potatoes, which are 99 percent water by weight. You let them dehydrate until they are 98 percent water. How much do they weigh now?
You can solve this with some logical thinking, or with algebra. But before you try, what do you think the answer will be? You will probably be very surprised…
Click to show/hide the solution
The amazing truth is that the reduction from 99% to 98% water means the potatoes have halved in weight! They now only weigh 50kg.
Let’s see if we can understand why using ratios.
Initially the ratio of water to solids is 99:1 (or 99% water). After dehydration it is 98:2 (i.e. 98% water). But the amount of solids has remained the same — specifically 1kg. Given our new ratio is 98:2, which is equivalent to 49:1, there must be 49kg of water to go with our 1kg of solids. This means the total weight has reduced to 49 + 1 = 50kg. Incredibly, 50kg of water has evaporated.
I am new to the blog can someone tell me who see’s these comments i know everyone can see the page about ratios but what about comments ??
Hi Max.
The comments on a public page can be seen by everyone. You can use the contact form on the front page or the welcome page if you want to send a private comment.