In this post I plan to hit you with not one, not two, but three bamboozlers! And they’re real beauties. Once again it will be infinity that is messing with our minds. I think you’ll have a lot of fun recognising just how crazy and exciting a concept it is.
We’ve all been confronted with, and grown to accept, some counterintuitive aspects of infinity. Specifically, I’d like you to think about the size of infinite sets. Now the size of a set is simply the number of items it contains — this is called the cardinality, and two sets are the same size if there is at least one way to match each element of one set with exactly one element of the other set, such that no elements in either set remain unmatched.
That makes perfect sense right? The set {1, 2, 3} is the same size as the set {A, B, C} because we can match 1↔A, 2↔B, and 3↔C. (There are, of course, other ways to match them up, but we only need to find one.)
However, things get more interesting when we deal with infinite sets.
For example, the set of all positive numbers {1, 2, 3, 4, … } is the same size as the set of all even numbers {2, 4, 6, 8, … }. As crazy as it sounds, throwing away every second element of the first set still leaves us with a set of the same size, because we can match up the elements like so: 1↔2, 2↔4, and 3↔6 etc. Any element in the first set has a single match in the second set, namely its double, and similarly any element in the second set can be matched with half its value in the first set. No element is left unmatched, and so, strange as it may seem, the sets are the same size.
Other sets of the same size as all positive numbers include the sets of all odd numbers, all multiples of 10, and even all fractions. It is only when we include irrational numbers, that is numbers like ![]() that cannot be written as fractions, that such a matching becomes impossible. (This was shown in 1891 by Gregor Cantor with his famous Diagonal Argument, and will probably be a topic I write up in future.)
that cannot be written as fractions, that such a matching becomes impossible. (This was shown in 1891 by Gregor Cantor with his famous Diagonal Argument, and will probably be a topic I write up in future.)
I am now going to describe a thought experiment that will illustrate some unexpected consequences of this property.
Bagging ping pong balls
Let me introduce Clark. He has a superpower that enables him to carry out what mathematicians call a supertask — i.e. a task that requires an infinite number of steps to be completed in a finite time. In our case, the time will be exactly one hour, starting at 11:00 and finishing at 12:00.
Clark has an infinite supply of ping pong balls, numbered in order from 1, and a bag to put them in.
At 11:00 he takes the first 10 balls, numbered 1, 2, 3, … 10, and places them in the bag. He then removes the ball numbered 10 from the bag, leaving the other 9 behind. Easy. No superpowers needed yet, and Clark should relax for a while and have a cup of tea, because it’s going to get harder.
After waiting 30 minutes, i.e. at 11:30, he places the next 10 balls, numbers 11, 12, … 20, into the bag, and removes ball 20.
After waiting a further 15 minutes (and so at 11:45) he places balls 21 to 30 in the bag, and removes ball 30.
Clark keeps doing this, always adding the next 10 balls then removing the 10th one, but waiting only half the previous wait time each step.
Clearly Clark will need to do this an infinite number of times to get through the infinite supply of ping pong balls. So will he ever finish?
To answer this, let’s think about a 1m string that is cut in half. We know that the two halves make the whole string, and so, obviously
![]()
Now take the second half, and divide it in half. We still have the whole string, but now the pieces show us that
![]()
Continue halving the last piece to get
![]()
then
![]()
and so on.
If you go on forever, you will have an infinite set of pieces of string, each half the length of the one before, but all still adding up to the original 1m length of string. This illustrates the fact that
![]()
and applies equally well to the times Clark is waiting between each step: half an hour, a quarter of an hour, an eight of an hour etc.
And so the whole process, although it involves an infinite number of steps, only takes one hour to complete. (And thanks to his superpower, Clark can carry out the infinite steps).
Question 1
At 12:00, when the process is complete, how many ping pong balls are in Clark’s bag?
Click to show/hide solution
Well, each step Clark adds 9 balls, and there are an infinite number of steps, so there will be an infinite number of balls in the bag. In fact, out of all the positive integers, only those balls numbered with a multiple of 10 will not be in the bag.
Bamboozler #1
OK. That was pretty obvious really. No bamboozling so far — just a little bit of concentration required to think clearly about the infinite process.
So let’s add a bit of confusion.
Suppose, while Clark is doing the experiment, his friend (and fellow superhero), Bruce, is also bagging an infinite number of ping pong balls. However, he uses a slightly different strategy.
At 11:00, Bruce takes the first 10 balls, numbered 1, 2, 3, … 10, and places them in a bag, but he removes ball number 1 from the bag. Then, at 11:30, he places the next 10 balls, numbers 11, 12, … 20, into the bag, but removes ball number 2. After 15 more minutes, at 11:45, he places balls 21 to 30 in the bag, and removes ball 3. And so on, each step adding the next 10 balls, but removing from the bag the ball with the smallest number.
Is Bruce’s approach essentially the same as Clark’s? Well, each time he is adding 10 balls and removing 1, so it certainly appears to be so.
Question 2
At 12:00, when Clark and Bruce compare their respective bags of ping pong balls, what do they see?
Click to show/hide solution
We know that Clark’s bag contains an infinite number of ping pong balls, but, incredibly, Bruce’s bag will be empty!
Yes — empty. Every ball will have been removed.
Think about it; what ball numbers can possibly remain? The balls are numbered 1, 2, 3 … to infinity, but each number corresponds to one of the infinite adding-removing steps and so each ball will have been removed. For example, ball 20 was removed on step 20, ball 1529 on step 1529, ball 1327821 on step 1327821. They’re all gone!
Bamboozler #2
Wow! That’s mad. Clark has an infinite number of ping pong balls, and Bruce has none. (For an interesting twist, suppose the experiment used dollar coins instead of ping pong balls, and you were allowed to keep whatever coins remained in the bag at 12:00…)
But it’s even weirder when you think what happens if they check before the time is up.
Question 3
Suppose Bruce and Clark check the bags every step instead of just at 12:00. What do they see?
Click to show/hide solution
Every time they check, prior to exactly 12:00, they will see they have the same number of ping pong balls.
It’s true — every single time they check, the number of balls will be exactly the same.
Only at 12:00 precisely, when the infinite process is completed, will there be a difference — and what a difference there will be! It will be like all of Bruce’s ping pong balls just vanish.
Bamboozler #3
Understanding and calculating the outcomes for Clark and Bruce depended on the numbering of the balls. So let’s now suppose a third superhero, Diana, was there and doing the same thing — 10 balls in, 1 ball out each step. However, Diana’s ping pong balls were not numbered and were completely indistinguishable.
Question 4
At 12:00, how many ping pong balls will be in Diana’s bag?
Click to show/hide solution
Sorry — no answer here. At this point we’ve pretty much crossed from Mathematics into Philosophy, so this question’s for you to think and argue about.

Discussion
Maybe you think this is all too unrealistic, because supertasks are not actually possible? Well, that doesn’t really matter in Mathematics. It is possible to think about them, reason about them, and study them. And this is true for many things in maths.
For example, do you believe in triangles? Are they real?
They’re not.
There is no such thing in the “real” world as a triangle. They exist only in our mathematical minds, just like infinity and supertasks and many other mathematical concepts. Every “triangle” we see is just an approximation — the sides are not really one dimensional and not exactly straight; the angles do not add exactly to 180 degrees etc. But this does not detract from the importance and necessity of studying triangles and their properties as mathematical entities.
So how does our ping pong problem relate to the mathematics of infinity and infinite sets?
- In each case we are adding an infinite number of balls and removing an infinite number of balls, but
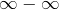 is undefined: it can be made to have many different answers. And that is indeed what we have found.
is undefined: it can be made to have many different answers. And that is indeed what we have found. - It is also illustrates the difference between showing the set of all positive integers and all even numbers are the same size by lining them up and matching the elements (this is essentially Bruce’s strategy):
![Rendered by QuickLaTeX.com \[\begin{array}{cccccc} 1 & 2 & 3 & 4 & 5 & \ldots\\ \updownarrow & \updownarrow & \updownarrow & \updownarrow & \updownarrow & \\ 2 & 4 & 6 & 8 & 10 & \ldots \end{array}\]](../../../../wp-content/ql-cache/quicklatex.com-d50e4c4cab1226ca827d3c640675dd05_l3.png)
compared to removing all the even numbers from the set of all numbers, and leaving an infinite set behind (this is Clark’s strategy):
![Rendered by QuickLaTeX.com \[1 \quad \cancel{2} \quad 3 \quad \cancel{4} \quad 5 \quad \cancel{6} \quad 7 \quad \cancel{8} \ldots\]](../../../../wp-content/ql-cache/quicklatex.com-bdad524800aef5f57f6a337312ba1513_l3.png)
Some further things to ponder
- You can construct a process that will leave any positive integer amount of balls in the bag by switching from Clark’s strategy to Bruce’s strategy at an appropriate time.
Try and come up with a strategy that leaves exactly 5 balls in the bag.
-
When Diana is performing the experiment, the balls are indistinguishable. Consider her kth adding/removing step.
- What is the probability of a random ball remaining in the bag after this step?
- What is the probability of a random ball remaining in the bag after this step and the next step?
- Can you use these results to calculate the probability of a random ball remaining in the bag after infinite steps?
- Does this calculation provide a way to answer question 4?
- In Bruce’s case, how does the final ball get removed to leave none, when he has always added 10 balls immediately before the removal?
- Imagine there was a gremlin in Clark’s bag, and when he tried to remove ball 10, the gremlin erased the 0 making it ball 1 and added a 0 to ball 1 (that is still in the bag) to make it ball 10. He did the same when Clark removed ball 20 — making it 2 and changing the other 2 into 20, and so on with ball 30 and ball 40 etc.
Does this gremlin’s renumbering mean the final number of balls in Clark’s bag changes to 0 (like Bruce)?
- If it does, how could it? He’s still removing exactly the same balls!
- If it doesn’t, what are the numbers on the balls left in the bag?
- Supertasks are clearly not physically possible. Do you think these paradoxes show that supertasks are not even logically possible?