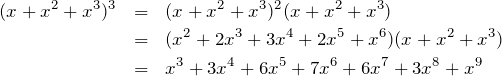Beginning in 2008, there was quite a hubbub in the Australian music industry. The publishing company, Larrikin Music, sued the iconic Australian band Men At Work claiming that the flute riff for their hit song Down Under was taken from a children’s song to which they owned the copyright — “Kookaburra Sits in the Old Gum Tree”. Bizarrely, they only acted after learning of the similarity from an episode of the ABC music quiz show “Spicks and Specks”. To much public consternation, the court ruled in favour of Larrikin Music.
Have a listen a see what you think.
| Down Under | Kookaburra |
This was by no means the first high profile popular music copyright case. Perhaps the most famous one involved George Harrison’s massive hit from 1970, “My Sweet Lord”, and The Chiffon’s 1963 song “He’s so Fine”.
| My Sweet Lord | He’s So Fine |
There’s also Ray Parker Jr’s theme from Ghostbusters, copied from the Huey Lewis and the News song “I Want a New Drug” — written after Huey Lewis had declined a request to write the movie theme!
| Ghostbusters | I Want A New Drug |
More recently Sam Smith with “Stay With Me” was forced to surrender a percentage of his royalties to Tom Petty because of similarities with his song “I Won’t Back Down”.
| Stay With Me | I Won’t Back Down |
A little bit of Internet searching will reveal many other examples, and the comedy group The Axis of Awesome made a wonderful parody of the multitude of similarities inherent in popular music in their “Four chord song”.
But this is a mathematics blog, so what has any of this got to do with maths?
Well, not too long ago I was listening to a discussion about this phenomenon on the radio, where it was suggested, and uncritically accepted, that “there are only so many songs you can write”.
Let’s see what we, as mathematicians, think of that assertion.
A Little Music Theory
When writing music, the duration (and hence the rhythm) is indicated by the appearance of the note. We will count note durations in half-beats, using numbers and musical notation as follows:
- 1 for a half beat (a quaver) — e
- 2 for a whole beat (a crotchet) — q
- 3 for one and a half beats (a dotted crotchet) — q.
- 4 for two whole beats (a minim) — h
Notes joined by a tie have their durations combined, so, for example, the note q-q lasts for 2 whole beats. Ties are used when the timing means a note crosses a barline or an important internal beat.
The pitch of a note (and thus the melody) is indicated by the vertical position on the stave, as shown below:
Modelling Music Mathematically
An important and practical aspect of mathematics is that it can be used to describe (technically model ) arbitrary processes, thus making it possible to analyse and understand those processes in a formal, quantitative way. And that means we can use mathematics to study questions like “How many different songs can there be?”
To make this problem accessible mathematically we need a way to represent the process of composition. I have chosen a very simple model based on three steps:
- Construct a rhythm (i.e. choose the individual note durations, and the overall characteristics of the beat).
- Attach notes to the rhythm to make a melody.
- Harmonise the resulting melody using chords (i.e. standard groups of related notes).
To further simplify, I will restrict the variety of tunes that we can construct by applying the following constraints:
- Each song is exactly 2 bars in length.
- The rhythm is made of notes of either 1, 2, 3 or 4 half-beat durations only, with no rests.
- Only the 12 white notes, from the A below middle C to the E an octave above, may be used in the melody. (By way of comparison, there are 88 notes on a standard piano.)
- The harmony is restricted to two chords in each bar, and the chords come from the most closely related three major chords (C, F and G) and their relative minors (Am, Dm and Em). Thus there are only 6 chords available to choose between.
This is clearly a very limited musical space, but before we decide to make things any more complicated, let’s see what kind of music we can make given these restrictions. If there really is a chance that composers can somehow use up a large proportion of all possible songs, no doubt under this simple model it will be even more likely.
Now let’s have a play
Head over to the activity at The Mathenæum that allows you to experiment composing (or getting the computer to compose) according to this model. You might be surprised at the results.
See you back here soon…

Eternal clock by R van der Steeg
creativecommons.org/licenses/by-sa/2.0
Time to do some calculations
OK then, back now? Completed the compositions for your first album perhaps? 
Let’s start to analyse our model, beginning with the simplest case. The shortest song we can write under this system has 3 notes only — a 3 minim tune in waltz time.
This is the only three note rhythm allowed under our rules, but what about the melody?
Amongst many others, we can have for example,
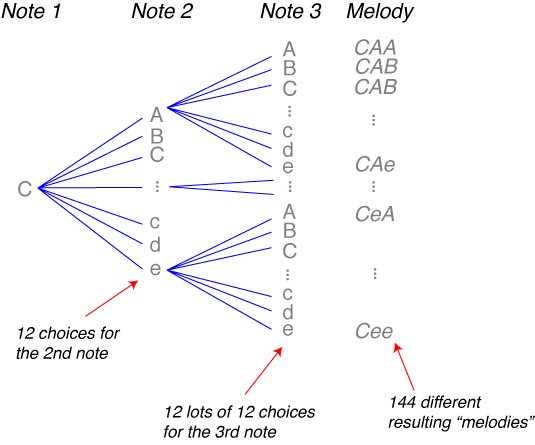
But just how many are there? When the computer composes, the first note is always middle C, and thereafter it makes choices from the 12 available notes. So the number of possible melodies is 1×12×12=144.
Do you see why? After taking middle C for the first note, any of the 12 notes can come next, and for each of those 12, there are another 12 choices for the third, leading to 144 possible melodies with this rhythm in total. It’s like branches of a tree: each choice follows one of 12 possible branches, and each end point is a different melody.
Analysing four note songs — counting arrangements
How about when we consider 4 note melodies instead of just 3? (We’ll stay with the waltz time for now.)
To get our required 12 half beats with 4 notes there are the following possible sets of individual note durations:
| 1344 | |
| 2433 | |
| 2424 | |
| 3333 |
But, each of these can be rearranged in many ways (well the first three can anyway) because the notes can come in any order. We need to count them all.
Calculating the number of arrangements is similar to our earlier calculation of the number of melodies, except in an arrangement, once something has been chosen it can not be chosen again. So each time there is one less thing to choose from.
With our 4 notes, we choose one of the four to go first — so there are 4 possibilities. Next we choose one of the remaining 3 to go second — that is 3 choices for each of the 4 initial choices, meaning 3×4=12 possibilities so far. Next we choose one of the remaining 2 for the third position, leaving just one for the last position (and thus just a single choice). Altogether this means we have 4×3×2×1=24 ways to arrange the four notes (or any 4 things in general).
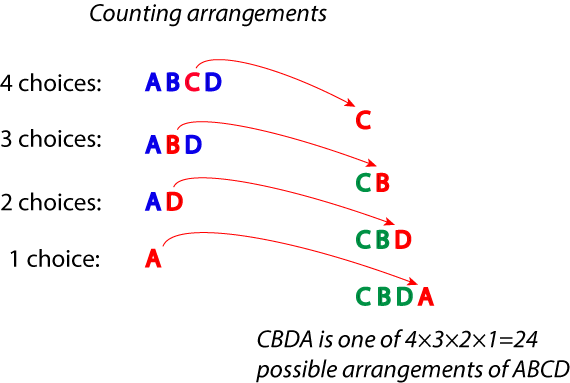
But, with 1344 for example, two of the numbers are identical, and this means some of the arrangements will be the same. Think about it — if we take 1344 and swap the last two 4s, we get 1344 again. Nothing has changed. We need to remove this double counting by dividing by 2×1=2, and so all in all there are 12 arrangements.
Just to be sure we are getting this right, let’s make a list:1344, 1434, 1443, 3144, 3414, 3441, 4134, 4143, 4314, 4341, 4413, 4431Yep, there’s 12 of them. (Good old maths!)
For 2433 we have the same situation — 4 numbers, but two are the same, so once again there are 12 arrangements, or 12 different rhythms with these 4 durations. 2424 has two identical pairs, so we need to divide by 2 twice leaving 6 arrangements, and 3333 is easy — there is only one arrangement.
Adding these all up we find there are 12 + 12 + 6 + 1 = 31 possible 4 note rhythms in waltz time for our composing.
Including melody and harmony in four note songs
What about the melody? Once again we will take the first note to always be middle C, and thereafter we make three consecutive choices from our 12 possible notes, so the number of melodies is 1×12×12×12=1728.
Putting it all together, 31 rhythms and 1728 melodies means 31×1728=53 568 tunes.
Hmmmm. This is growing quite fast, yet we’ve only just begun considering the possibilities for the tune, and haven’t considered the harmony at all.
The computer’s choice of harmony is not purely random because that would lead to many discords. Instead it chooses a chord that matches well with the notes in each half bar. With the notes we are using and the available chords, each note matches with either 2 or 3 of the chords. For example, a C note can be harmonised by a C chord, an F chord or an Am chord, since they all include a C and the other chords do not. Similarly, a B note can be harmonised by a G chord and an Em chord, but none of the others. Since 7 of our 12 notes match 3 of the chords, and the other 5 match with 2 of the chords, we can say that on average we have approximately 2.6 choices of chord at each of the 4 points at which we apply a harmony. Using the same method that we used to count melodies you can see that there are, on average, 2.6×2.6×2.6×2.6 ≈ 45 harmony possibilities for each melody, and thus well over 2 million (from 53 568×45) different harmonised 4 note tunes!
The Complete Calculation
To fully calculate the number of possible compositions, we need to consider all the melodies; from 3 notes right up to the maximum of 16. The greatest rhythmic variation comes in the case of 9 notes in 4/4 time — 4950 possible rhythms, and the greatest melodic variation comes, unsurprisingly, when there are most notes — 16 notes giving 15 021 574 586 368 possible melodies. Putting these two aspects together, it is actually the case of 15 notes (i.e. 14 quavers and one crotchet) that has the maximum melodic variation: 19 258 776 968 232 960 possible tunes (i.e. nearly 20 quadrillion tunes with 15 notes).
The following two tables give a complete breakdown of all the cases for each timing.
Full results for 3/4 time
| Notes | Rhythms | Melodies | Tunes | Including harmony |
|---|---|---|---|---|
| 3 | 1 | 144 | 144 | 6 413 |
| 4 | 31 | 1 728 | 53 568 | 2 385 762 |
| 5 | 155 | 20 736 | 3 214 080 | 143 145 755 |
| 6 | 336 | 248 832 | 83 607 552 | 3 723 636 672 |
| 7 | 413 | 2 985 984 | 1233211392 | 54 923 640 912 |
| 8 | 322 | 35 831 808 | 11537842176 | 513 861 860 736 |
| 9 | 165 | 429 981 696 | 70 946 979 840 | 3 159 771 690 240 |
| 10 | 55 | 5 159 780 352 | 283 787 919 360 | 12 639 086 760 960 |
| 11 | 11 | 61 917 364 224 | 681 091 006 464 | 30 333 808 226 304 |
| 12 | 1 | 743 008 370 688 | 74 300 8370 688 | 33 091 427 155 968 |
| Totals | 1 490 | 810 554 586 192 | 1 791 692 205 264 | 79 796 748 509 722 |
Full results for 4/4 time
| Notes | Rhythms | Melodies | Tunes | Including harmony |
|---|---|---|---|---|
| 4 | 1 | 1 728 | 1 728 | 76 960 |
| 5 | 65 | 20 736 | 1 347 840 | 60 028 865 |
| 6 | 546 | 248 832 | 135 862 272 | 6 050 909 592 |
| 7 | 1 918 | 2 985 984 | 5 727 117 312 | 255 069 112 032 |
| 8 | 3 823 | 35 831 808 | 136 985 001 984 | 6 100 912 713 024 |
| 9 | 4 950 | 429 981 696 | 2 128 409 395 200 | 94 793 150 707 200 |
| 10 | 4 455 | 5 159 780 352 | 22 986 821 468 160 | 1 023 766 027 637 760 |
| 11 | 2 882 | 61 917 364 224 | 178 445 843 693 568 | 7 947 457 755 291 648 |
| 12 | 1 353 | 743 008 370 688 | 100 529 032 5540 864 | 44 772 700 942 024 704 |
| 13 | 455 | 8 916 100 448 256 | 4 056 825 703 956 480 | 180 679 192 271 585 280 |
| 14 | 105 | 106 993 205 379 072 | 11 234 286 564 802 560 | 500 342 378 598 236 160 |
| 15 | 15 | 1 283 918 464 548 864 | 19 258 776 968 232 960 | 857 729 791 882 690 560 |
| 16 | 1 | 15 407 021 574 586 368 | 15 407 021 574 586 368 | 686 183 833 506 152 448 |
| Totals | 20 569 | 16 807 659 899 548 608 | 51 165 905 061 007 296 | 2 278 780 276 227 166 233 |
My head’s spinning! Just tell me how many.
Ok, ok. Adding these together, we have a total of 22 059 rhythms (from 3 notes to 16 notes), leading to more than 50 000 000 000 000 000 tunes (that’s 16 zeroes — 50 quadrillion!). Including harmonies, we end up with a final number of 2 300 000 000 000 000 000 songs (2.3 quintillion). And remember, these are not just random arrangements, but we have used rules to greatly increase the chance of a resulting tune sounding musical (matching harmony, starting on C etc).
That’s a lot of tunes! A very lot. So many that it’s actually quite difficult to imagine, but this might help.
- If we were to only keep one in every million songs (assuming the others are too similar or not musically interesting) we would still have more than 2 trillion songs in total.
- If we started composing in this way the very instant the universe began, writing one song every second right up until now, we would still be less than 20% through all the possibilities!
- If we printed out all the songs in a line, each song taking up 15cm, the length of paper would go from Earth to Proxima Centauri (the nearest star after the Sun — about 4.23 light years away) and back more than 4 times. That’s about 36 light years.
Extension: How did I calculate all those numbers?
The hard calculation is determining the number of possible rhythms, but we can see how to approach it by looking at the following three similar problems.
- If each choice must be a 1 or a 2, in how many ways can you make two choices and get a sum of 3?
- If each choice must be a 1 or a 2, in how many ways can you make three choices and get a sum of 5?
- If each choice must be a 1, 2 or 3, in how many ways can you make three choices and get a sum of 6?
These are all small enough to be solved by brute force, but instead let’s consider the apparently unrelated algebra:
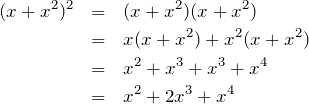
Each term in the this expansion can also be seen as the result of making two choices from the ![]() term, that is choosing either
term, that is choosing either ![]() or
or ![]() . If we choose
. If we choose ![]() twice and multiply, we get
twice and multiply, we get ![]() , and since there is only one way to choose
, and since there is only one way to choose ![]() twice, the
twice, the ![]() term in the final answer has a coefficient of 1. Similarly, there is also only one way to choose
term in the final answer has a coefficient of 1. Similarly, there is also only one way to choose ![]() twice, and this time the product makes the
twice, and this time the product makes the ![]() term. However, there are two ways to choose an
term. However, there are two ways to choose an ![]() and an
and an ![]() , either
, either ![]() first then
first then ![]() , or in the opposite order, leading to the coefficient of 2 in the
, or in the opposite order, leading to the coefficient of 2 in the ![]() term.
term.
The coefficient in the final expression is telling us how many ways there are to get each combination, but there is more information there — the final power is giving the sum of the individual powers (by the index law ![]() ).
).
And this second observation is what connects it to our problem.
- How many ways to add to 2?
1 — choose 1 twice, or choose twice and get the
twice and get the  .
. - How many ways to add to 3?
2 — there are two ways to choose one of each, hence the coefficient of 2 in the term, and the sum is 3 because the power of
term, and the sum is 3 because the power of  is 3.
is 3. - How many ways to add to 4?
1 — choose 2 twice, or choose twice and get the
twice and get the 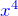 .
.
The middle case is the solution to our first example problem.
To solve the second problem, that is three choices of 1 or 2 with a sum of 5, we follow the same approach but this time we raise the binomial expression to the power 3 (each product is one choice) to get
![]()
We can then simply read off the coefficients and powers to find that there is 1 way to add to 3 (111), 3 ways to get a sum of 4 (112, 121, 211), 3 ways to get a sum of 5 (122, 221, 212), and 1 way to get a sum of 6 (222). The sum of 5 case is the solution to the second problem.
This is a beautiful and powerful technique, and is known as a Generating Function.
Try using a generating function to solve the third example problem. (Click here for the solution.)
Counting the possible rhythms using a generating function
For our composing problem we can use this approach. For example, to calculate the number of rhythms made up of 8 notes that sum to 12, we need to look at the coefficient of the ![]() term in the expansion of
term in the expansion of
![]()
(Wolfram Alpha can help with this). The answer of 322 matches the value in the 2nd column of the 3/4 table for 8 notes.
Then, as before, 8 notes but starting on middle C means choosing a note from the 12 available 7 times, leading to 127=35 831 808 possible melodies (which you can see is the corresponding value in the third column). Multiplying these two together will give the total number of 8 note tunes.