Probability is all about counting. The basic problem in probability is to work out how likely something is by counting how many ways it can happen, and then comparing that number to how many ways any ways anything can happen. Divide the first number by the second ad you have the probability.
Simple right?
For example, what is the probability of getting heads when flipping a coin? Well, let’s work it out using three steps:
- How many ways can what are we interested in, i.e. flipping heads, happen?
Only one way. - How many ways can anything happen?
Well, the only possibilities are flipping heads or flipping tails, so there’s two ways. - Divide the first number by the second to get the probability.
![Rendered by QuickLaTeX.com \[P(\mbox{heads})=\frac{1}{2}.\]](../../../../wp-content/ql-cache/quicklatex.com-7cb900a9b7a548ed7d4b1a609b144c18_l3.png)
As another example, what is the probability of randomly choosing an orange from a bucket containing 5 apples and 3 oranges?
- How many ways can we choose an orange?
We can choose any one of the 3 oranges, so there are 3 ways. - How many ways can anything happen?
There are 8 pieces of fruit in all, so 8 ways. - Divide the first number by the second to get the probability.
![Rendered by QuickLaTeX.com \[P(\mbox{orange})=\frac{3}{8}.\]](../../../../wp-content/ql-cache/quicklatex.com-e4dd72418404125168c3a105af020331_l3.png)
The probability is always a number from 0, when there is no way for the outcome of interest to happen — it is impossible, to 1, when the outcome of interest is certain — whatever happens is included in that outcome.
Of course it is not always quite so straightforward. What kinds of things can go wrong? Well, you can miss some possibilities in your counting, or you can accidentally count some things twice. Another trap is failing to properly take account of things not being equally likely. In our second example we could not simply have said there are two things that can happen — choose an orange or choose an apple, because they are not equally likely. To calculate the probability correctly we needed to consider each apple and orange separately.
Conditional Probability
Where probability really gets tricky, and often quite counterintuitive, is when the problem has the form: given something has happened, what is the probability that something else also happens. This is known as conditional probability and the first case we will look at comes in the form of a puzzle.
Suppose you meet a man and a boy in the street, and the man tells you “This boy is the elder of my two children.” Going a little further you meet a second man, who simply tells you “This boy is one of my two children.”
Calculate the probability that each man has two sons.
Both of these are questions of conditional probability. The “given” in each case is that the man has a son, but the details are slightly different. Your first instinct might be that there is no real difference between the two situations, but if we analyse them carefully we will see that they are in fact quite different.
For the first man, the question is simply is his younger child a boy? There are only two possibilities, boy or girl, and we can consider them equally likely, so the probability is ![]() .
.
Now how about the second man? The crucial difference in this case is we don’t know if the boy we meet is the first or second child. To solve this we need to think of all the possibilities — we can summarise them using a tree diagram as follows:

If we follow the branches of the tree all the way from the left to the right hand edge, we can see how each of the possible 2 child outcomes occur — you could first have either a boy or a girl, then which ever you had first, the second child is also either a boy or a girl. This shows us that there are four equally likely outcomes: two boys, a boy then a girl, a girl then a boy, or two girls.
For the first man we know the first child was a boy, so we do not need to consider the bottom half of the diagram at all. But for the second man, all we know is that he had a boy. That’s enough for us to not consider the girl+girl outcome, but we don’t know anything else. Specifically, we don’t know if the boy was his first or second child. So, unlike the first man, we need to count all 3 of the remaining outcomes, and since 2 of the 3 include a girl, the probability that he has no girls is the remaining 1 only. The probability that he has two sons is therefore ![]() .
.
Isn’t that surprising? The second man’s other child is twice as likely to be a daughter than a son. Surprising, but true.
If it doesn’t make sense, reread the explanation and make sure you understand. It’s about to get a lot more confusing.
The Prosecutor’s Fallacy
A fallacy is a logical argument that appears valid, but is actually false, and misunderstanding probability leads to a couple of important fallacies that can have significant consequences in everyday life.
Suppose, in a city of 1 million people, a serious crime has been committed. Investigators comb the scene and are able to recover some DNA evidence that shows, to their delight, that the perpetrator has a particularly rare characteristic, present in only 1 of every 10 000 individuals. Surely that will make it easier to catch the culprit!
A little while later they have brought a suspect to trial, during which the prosecutor declaims to the jury:
The genetic signature of the criminal, found at the scene of the crime, is extremely rare. The chance of someone carrying this DNA is just 1 in 10 000 — only 0.01%. Yet the accused has this DNA, and this alone shows how likely is his guilt!
Now suppose you are sitting in the jury, listening to this impassioned speech. Do you accept the argument? Does it move you towards a guilty verdict? I certainly hope not! Let’s bring some mathematics to bear.
There are 1 million people in the city, so a frequency of 1 in 10 000 tells us that the number of people in the city with the particular DNA signature is 100. Now, the crucial point is that 99 of the 100 people with that DNA are actually innocent. The chance of any of them being guilty, including of course the accused in the trial, is only 1%. The prosecutor is making an elementary mistake in probability. Fortunately, thanks to your presence on the jury, mathematical thinking prevails, and no one is convicted due to The Prosecutor’s Fallacy.
The Base Rate Fallacy
This time, suppose you have invented a stolen car scanner — a device that can scan any car that passes and instantly determine, with an incredible 99% accuracy, whether or not the car has been stolen. Unsurprisingly, your invention gains the attention of the police, who install it on the Sydney Harbour Bridge.
On one particular day, the policewoman who attends the device, and knows that it is 99% accurate, is wondering about the likelihood that a car she has pulled over (after it registered on the scanner) is indeed stolen? Well, the device is 99% accurate, so there must be a pretty good chance that the car has been stolen right? Let’s calculate some probabilities and see.
First we need some data. The daily volume of cars on the Sydney Harbour Bridge is approximately 100 000, and in 2013 there were on average 45 cars stolen per day. Using these figures we can estimate that out of the 100 000 cars that cross the bridge on any day, maybe 10 of them are stolen. What do these values mean for your invention? Let’s further suppose that the device never fails to correctly scan a stolen car, so all 10 stolen cars that pass register as stolen. In addition, 99 990 innocent cars are scanned, 99% of which safely pass the scanner, but 1% are scanned as stolen in error. And here’s the rub — 1% of 99 990 is essentially 1 000 cars! That’s right, every day we can expect 1 000 cars to be incorrectly scanned as stolen, even though the device is 99% accurate. This means that given any particular car that has been scanned as stolen and pulled over, the probability that it is actually stolen is 10 divided by 1 010, or 0.99%. That’s right, less than one percent of the cars that register as stolen, are actually stolen cars.
Hmmmm. I’m afraid I have to say, that even with an accuracy of 99%, your device is not actually that useful. Our tendency to think otherwise is an example of the Base Rate Fallacy.
This is also a very important consideration in medicine when assessing the results of diagnostic tests — specifically what exactly does it mean to return a positive test for a rare disease?
Bamboozler: Does it matter when the son was born?
For our bamboozler, we will return to the problem of a man with two children. We have seen that if we know that the elder child is a boy, the probability of two sons is one-half, but if all we know is that one of the children is a boy, the probability of two sons is only one-third.
Now suppose you meet a third man, also with his son, who tells you:
This boy is one of my two children. He was born in the morning.
What difference could the time of his son’s birth possibly make to the probabilities?
Believe it or not, it actually changes the answer.
Click to show/hide explanation
Just like for the second man earlier, we need to consider all the possibilities, but instead of just boy or girl, we have to incorporate the time of day. This leads to 4 equally likely possibilities for each child:
- a boy born in the morning,
- a boy born in the afternoon,
- a girl born in the morning,
- a girl born in the afternoon.
Four possibilities for each child means 16 possibilities for his two children. However, we know that at least one of his children is a boy born in the morning, so we can summarise the situation using the following table where a ![]() indicates an outcome we need to consider. (Across the columns we have the possibilities for the first child, and down the rows we have the possibilities for the second child.)
indicates an outcome we need to consider. (Across the columns we have the possibilities for the first child, and down the rows we have the possibilities for the second child.)
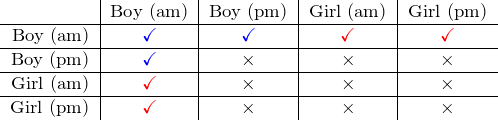
There are 7 equally likely outcomes that include a boy born in the morning, and to work out the probability that this third man has two sons we will again use our three step approach.
- How many outcomes include two boys?
3 of the included outcomes (the blue ticks) include two sons. - How many ways can anything happen?
Given we know he has at least one son born in the morning, there are 7 outcomes (all the ticks) in total to consider. - Divide the first number by the second to get the probability.
![Rendered by QuickLaTeX.com \[P(\mbox{two sons})=\frac{3}{7}.\]](../../../../wp-content/ql-cache/quicklatex.com-40508b488b8285bee47952266b46e470_l3.png)
Notice that this probability lies between the earlier two answers.